Characteristics of Submicron Heterogeneities in Aqueous Solutions of Sugars. Possible Cryoprotection Factor
- Affiliations
-
- 1. Institute of Cell Biophysics RAS FRC PSCBR RAS
- Published:
- 2025-03-30
- Keywords:
- aqueous solutions, submicron heterogeneities, sugars, cryoprotection, light scattering methods
Abstract
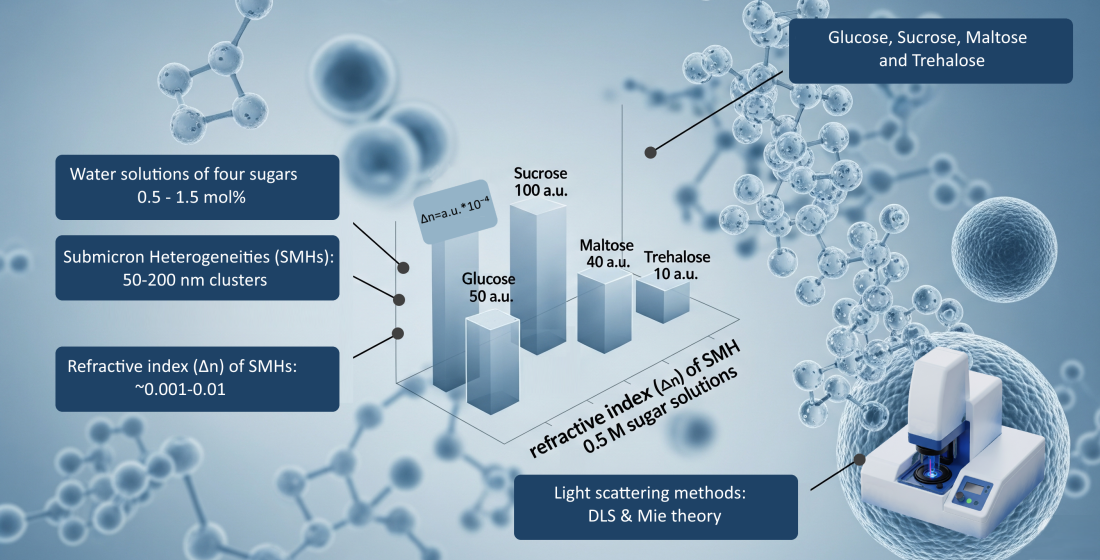
The present work is devoted to the study of submicron heterogeneities (SMH) spontaneously formed in aqueous solutions of low molecular weight organics. SMHs of about 100 nm in size were found in solutions of four sugars: glucose, sucrose, maltose and trehalose at concentrations of 0.5 - 1.5 mol%. In addition, using a combination of methods of dynamic light scattering, static multi- angle light scattering and Mie theory, the refractive indices of SMHs were determined; they turned out to be almost identical to those of the solutions containing them, differences are 0.001 - 0.01. These values are anomalously small for ordinary colloids, which explains the imperceptibility of SMHs. The concentration of SMHs increases with increasing concentration of sugars. Judging by the values of differential refractive indexes of SMH in different solutions, the composition and structure of SMH can be very different even for structurally similar molecules, such as disaccharides. At concentrations of sugars ~10 weight%, typical for cryoprotective solutions, the trehalose solution has a much lower value of the differential refractive index of SMHs and their highest concentration compared to solutions of other sugars. The role of SMHs in cryoprotection processes was suggested for the first time, which may explain the greatest cryoprotective efficiency of trehalose among other low molecular weight sugars.
Full text
Introduction
Many physical, chemical, biological and related studies are carried out with samples in the form of aqueous solutions, as they are convenient models of various natural systems. According to chemical classifi- cation, solutions are divided into two types, true and colloidal, which are considered fundamentally different from each other. True solutions are homogeneous, whereas at the supramolecular scale, colloidal solutions are inhomogeneous in composition and density. However, as early as 1972, Vuks and Shurupova found anomalous light scattering in a typical true water/tret-butanol solution associated with the presence of heterogeneities and interpreted them as unstable clathrate-like structures [1]. Later it was repeatedly shown that in this and many other solutions certain heterogeneities were formed, which however were differently named and interpreted [2-7]. Now they are found in more than 100 different solutions [8-10], which indicates the universality of this phenomenon. Most of them are aqueous solutions of low molecular weight organics. Surprisingly, up to now all these solutions are considered to be true solutions.
The point is that the discussed heterogeneities are in most cases difficult to identify because of their very small optical and density contrast relative to the medium. This fact makes impossible their revealing by conventional methods, such as small-angle X-ray [11] and neutron scattering [12]. Light scattering methods, namely dynamic light scattering (DLS) and multi-angle static light scattering, have proved to be the most sensitive [8, 9, 13-16]. There have been attempts to show the applicability of other methods: polarimetry [17], compressibility measurement [5], cryomicroscopy [18], but they are much less informative.
Light scattering methods show that these heterogeneities have sizes from tens to hundreds of nanometers; that is why in some papers they were named submicron heterogeneities (SMH) [19-21]. In addition to measuring the sizes of SMHs, some works [15, 19] proposed methods for determining their concentration and refractive index.
Despite the obvious fact of the presence of SMHs in many aqueous solutions of organics and a half-century history of their study, the nature of SMHs is largely unclear. Apparently, SMHs represent areas of the solution with an increased content of the organic component, behaving as Brownian particles [22]. They have a spherical shape and are able to partially permeate water through them [19]. SMHs are stable formations; at least in some solutions, their stability has been experimentally confirmed for months [9, 22] and even years [23] after solution preparation.
Different mechanisms of stability preservation have been proposed, but there is no universally accepted point of view. According to one version, SMHs are formed as a result of binding of dissolved molecules by hydrogen bond bridges from water molecules [10]. According to another version [15, 24-26], SMHs are formed due to the decomposition of the spinodal-type solution, which occurs under the influence of dichotomous noise of twinkling hydrogen bonds between water and organic molecules.
Some authors believe that SMHs are formed in aqueous solutions only in the presence of hydrophobic components [11, 12, 22, 23]. Hydrophobic impurities, at least in trace amounts, are always present both in nature and in reagents, even of high purity. It is also difficult to avoid the influence of dissolved air gases and plastic laboratory glassware. According to one hypothesis, SMHs consist of a hydrophobic enriched core around which a shell enriched with organic molecules is formed [14]. Or similar micelles with sizes of about 10 nm are formed, which then combine into larger clusters [27]. At the same time, the presence of hydrophobic components in the composition of SMHs contradicts the results of recent work [20], indicating the hydrophilic nature of SMHs.
It has also been hypothesized that SMHs are air bubbles [5, 28, 29], although much more publications have been devoted to disproving this hypothesis [13, 30-33]. Perhaps the presence of bubbles in aqueous solutions of organics was assumed by analogy with aqueous solutions of salts, in which ion-stabilized bubbles were formed [34-37]. In our work [19], it was shown that bubbles of submicron sizes could indeed be present in such solutions, but in very small amounts, and the bulk of SMHs were of a different nature. They were also spherical, but had a much smaller optical and density contrasts.
A filtering procedure has often been used in studies of SMHs; it usually eliminates them [11, 13, 38, 39]. In some cases they are either formed again [18, 21, 40] or are not formed [21, 22]. So filtration simply destroys SMHs, rather than literally filtering them out. This gives a convenient opportunity to conduct comparative studies of solutions of the same chemical composition, containing and not containing SMHs.
Among the papers describing SMHs in aqueous solutions of organics, there are very few devoted to sugars. Sugars belong to one of the four fundamental types of biomolecules, carbohydrates [41], which play an indispensable role in many biological processes related to energy [42], cell adhesion [43], intercellular interaction [44], bioprotective mechanisms [45], and others. All these processes have been studied incompletely yet, and the possible role of SMHs in biological processes has not been considered at all.
In the present work, SMHs formed in aqueous solutions of a number of sugars at different concentrations were studied by light scattering methods. Scattering intensities in these solutions, hydrodynamic diameters of SMHs and their refractive indices were determined. The characteristics of SMHs in solutions of different sugars are compared. The possible role of SMHs in cryoprotection is discussed for the first time.
Materials and methods
2.1. Reagents and preparation of solutions
The following reagents were used: D(+)-glucose anhydrous #131341 (Panreac, Spain), D(+)-saccharose anhydrous #141621 (Panreac, Spain), D(+)-maltose monohydrate #LC-5054.4 (NeoFroxx, Germany), D(+)-trehalose dihydrate #A1742 (Panreac, Spain) and MilliQ water (Millipore, Germany). Solutions of each sugar were prepared at concentrations of 0.5, 1 and 1.5 mol% by weight method. Dissolution was carried out by smooth manual inversion of a 20 mL test tube (Sarstedt, Germany) until complete visual dissolution at room temperature. Each solution was prepared at least 3 times.
2.2. Dynamic Light Scattering (DLS) method
A widely known DLS method [46] was employed using the Photocor Complex equipment (Photocor Ltd, Russia). Measurements of scattering intensity in solutions of laser radiation with a wavelength λ =451 nm with a power of 50 mW were performed at an angle of θ=140˚. An avalanche photodiode operating in the photon counting mode was used as a detector, so the intensity was measured in kHz (thousands of counts per second).
In addition to determining mean values of the scattering intensity, the temporal fluctuations of the intensity were measured, from which the autocorrelation function G2(τ) was determined. In the case of monodisperse Brownian particles, this function is related to their diffusion coefficient D as follows:
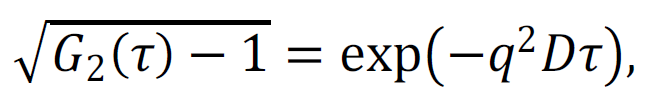 |
(1) |
where τ is the correlation time and q is the modulus of the scattering vector:
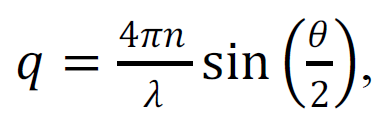 |
(2) |
n – is the refractive index of the solution. From relations (1) and (2), D is determined, from which the hydrodynamic radius Rh of the particles can be calculated using the Stokes-Einstein relation:
| (3) |
where k is the Boltzmann constant, T is the absolute temperature, η is the dynamic viscosity of the solution. Since in practice there occurred a polydisperse distribution of SMH sizes, we determined not one diffusion coefficient from the correlation function, but their distribution, from which the size distribution of SMHs was calculated using the program DynaLS (Photocor Ltd,, Russia).
Formula (3) relates the particle size to its diffusion coefficient under the assumption that it is a rigid sphere. The sphericity of SMHs in solutions of sugars was previously confirmed [19] by measuring the scattering depolarization. However, from the study of SMHs it is evident that they are hardly rigid particles, but rather represent analogues of microdroplets. This follows from some publications [15, 24-26] and from many other works that show the destruction of SMHs by filtration [13,32]. For the emulsion type of particles, more correct is the analog of formula (3) obtained by taking into account the generalized Stokes force [47], in which the viscosity of the microdroplet substance η' is also taken into account:
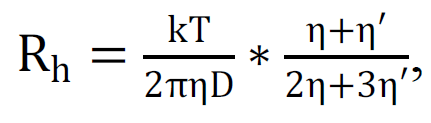 |
(4) |
In our case, η'≈η so the approximate hydrodynamic radius of the particles can be calculated by the formula:
| (5) |
Formula 5 gives Rh values 20% higher than those determined by the standard DLS methodology (using Formula 3). In reality, we do not know what the viscosity of the SMH substance is, so the Rh calculated using Formulas 3 and 5 can be considered as a lower and an upper limit. In this work, Formula 5 was used in all cases for certainty and the size was defined as 2Rh, i.e. as a hydrodynamic diameter.
All measurements were carried out at a stabilized solution temperature of 25±0.2˚C. Each separately prepared solution was measured at least 6 times.
2.3. Determination of the difference refractive index of the SMH relative to the surroundings
In the present work, the method of multi-angle static light scattering was also applied. For this purpose, the Mastersizer 2000E (Malvern, UK) was used, which, in fact, is a diffraction analyzer that allows for determining the particle size distribution in liquid media. To do this, the scattering indicatrix of laser radiation (with a wavelength of 633 nm) in the sample is measured and analyzed using Mie theory. In addition to the scattering indicatrix of the sample containing the studied particles, it is also necessary to measure the background indicatrix of the same liquid medium, but without particles. As a background sample, we used the same solutions passed through a filter with a pore diameter of 20 nm (much smaller than the SMH size) Anotop 10 0.02 mkm (Whatman GmbH, Germany). After filtration of the solutions, the absence of SMHs for one hour was verified by the DLS method. This time was sufficient for the measurement of the scattering indicatrix. The scattering indicatrix of each separately prepared solution was measured at least 5 times.
According to Mie theory, the calculation of size distributions from the indicatrix is only possible at known values of complex refractive indices of liquid medium and particles contained in it, SMH in this case. The imaginary part of the refractive index is responsible for the absorption of radiation, which is negligibly small for sugar solutions at the wavelength used. Therefore, we used only the real part. The refractive indices of the medium were determined from reference data [48], and the refractive indices of SMHs were initially unknown. But in the present work, the opposite problem was solved. The refractive index of the SMH was chosen in such a way that the sizes of the SMH calculated by Mie theory were close to the sizes determined by the DLS method. Thus, we determined not the size distributions of SMHs, but their important optical parameter, i.e. the refractive index. Details of this experiment and examples of its application can be found in [19].
It is noteworthy that according to the Babine principle, only on the basis of scattering data it is impossible to distinguish two cases when the refractive index of particles is higher and lower than that of the medium. Only the absolute value of the difference refractive index can be determined. But since SMHs are considered to be formations with increased sugar content, the refractive index should be higher than that of the medium, which makes the choice unambiguous. The version of the presence of stable solution regions with reduced concentration of sugars is considered as unrealistic in the present work.
ResultsThe characteristic size distributions of optical heterogeneities in the studied solutions are shown in Figure 1. The peak of about 1 nm belongs to the monomolecular fraction of sugars, and the peak of about 100 nm belongs to SMH.
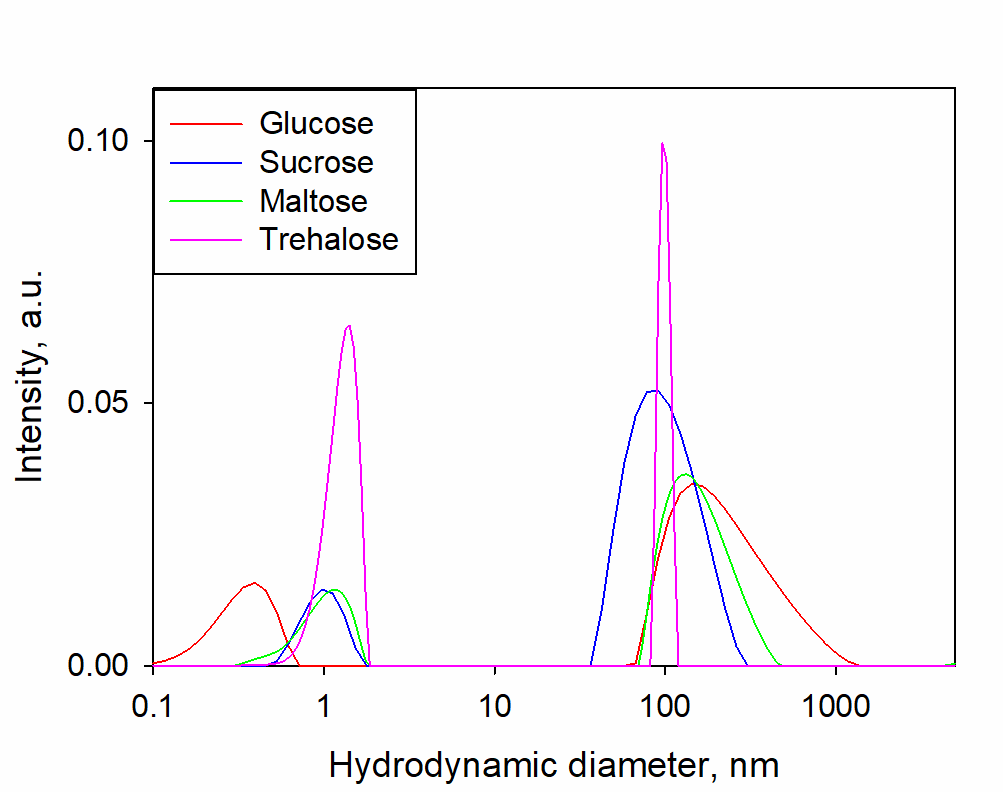
Figure 1. Typical size distributions of optical heterogeneities determined by the DLS method in solutions of glucose, sucrose, maltose, trehalose in the concentration range of 0.5-1.5 mol%. Changes in the distributions according concentration are insignificant and therefore are not shown.
The concentration dependences of the hydrodynamic diameters of SMHs in solutions of sugars are shown in Figure 2; the scattering intensities in these solutions are shown in Figure 3. Table 1 shows the values of the difference refractive indices of SMHs relative to the mean values of the solutions in which they are found.
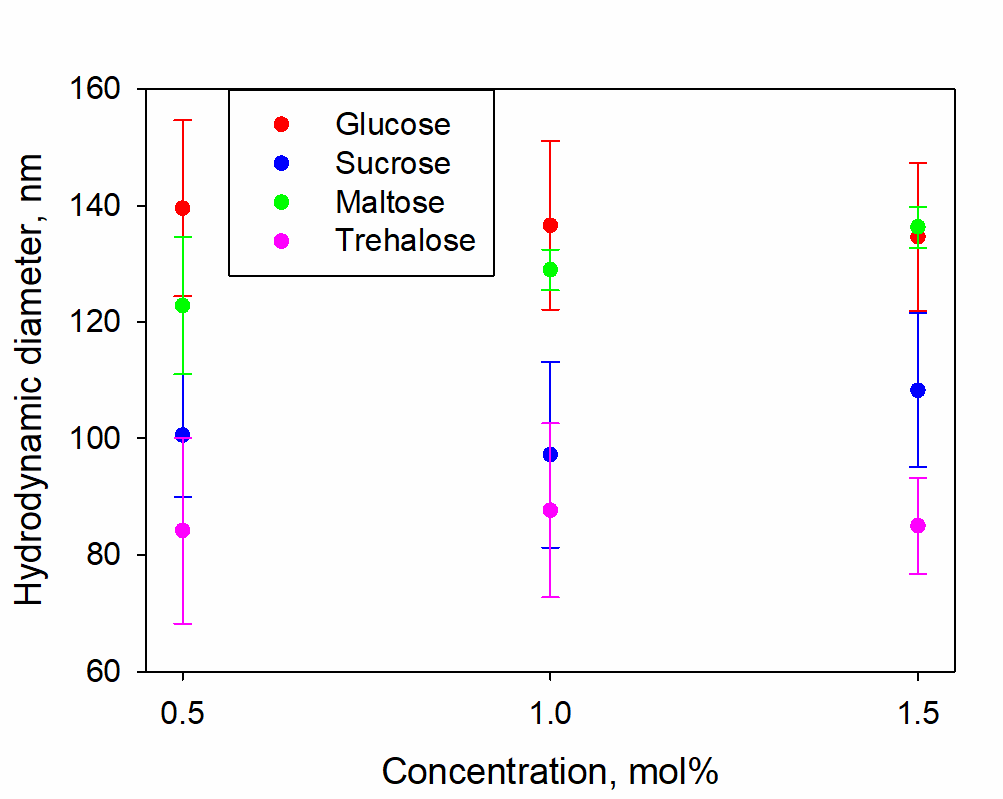
Figure 2. Hydrodynamic diameters of SMHs in solutions of glucose, sucrose, maltose and trehalose with concentrations of 0.5, 1, 1.5 mol%
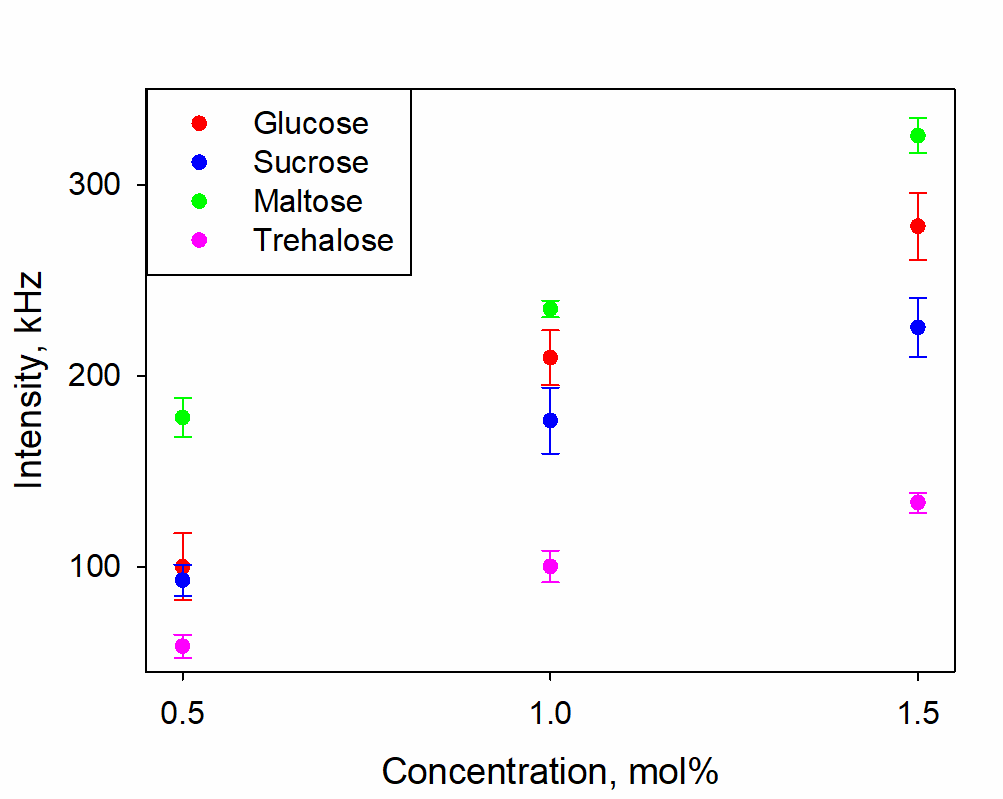
Figure 3. Scattering intensity of radiation in glucose, sucrose, maltose and trehalose solutions with concentrations of 0.5, 1, 1.5 mol%
Table 1. Difference refractive index (Δn) of SMH relative to the mean value in glucose, sucrose, maltose and trehalose solutions with concentrations of 0.5, 1, 1.5 mol%
|
Concentration, mol% |
0.5 |
1 |
1.5 |
|
Glucose |
50x10-4 |
30 x10-4 |
20x10-4 |
|
Sucrose |
100x10-4 |
30 x10-4 |
5x10-4 |
|
Maltose |
40x10-4 |
20 x10-4 |
30x10-4 |
|
Trehalose |
10x10-4 |
30 x10-4 |
20x10-4 |
Figure 1 shows the presence of two well-defined types of heterogeneities in the solutions considered: individual sugar molecules (~1 nm) and SMHs (~100 nm). When the concentration of sugars is varied in the range of 0.5-1.5 mol%, the size distributions do not change significantly, neither in the ratio of the fractional contribution nor in the size of SMHs (Figure 2).
Figure 3 shows that as the concentration of sugars increases in the 0.5-1.5 mol% range, the scattering intensity also becomes higher. With weakly varying size distributions, this can be attributed to two factors: increasing Δn and increasing concentration. Table 1 shows that Δn either decreases or remains approximately the same with increasing concentration for all sugars. Therefore, the increase in the scattering intensity can only be attributed to an increase in the concentration of SMH.
It is noteworthy that the obtained Δn values ~ 0.001-0.01 (Table 1) are anomalously small compared to conventional colloidal solutions. For example, in milk, that is basically an emulsion of fat in water, Δn≈0.14. The scattering capacity of a spherical heterogeneity in the medium is determined by the formula:
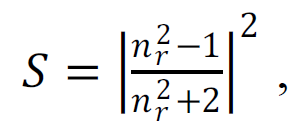 |
(6) |
where nr is a relative refractive index. Thus, for comparable sizes, the scattering capacity of fat droplets is 103 to 104 times greater than, for example, of SMHs in trehalose solutions. This provides a quantitative understanding of why this type of heterogeneity is generally undetectable when working with organic solutions. Specialized light scattering techniques are needed to record SMHs.
Table 1 shows that the concentration dependences of Δn can vary significantly in the solutions of different sugars. As the concentration of glucose and sucrose increases, Δn decreases monotonically, whereas for maltose and trehalose this dependence is non-monotonic. The value of Δn is directly related to the difference between the sugar concentration in SMH and the solution average. Therefore, the composition (and, possibly, the structure) of SMH in organic solutions can differ greatly even at insignificant differences in the structure of organic molecules and at their similar concentrations.
It is noteworthy that at 0.5 mol% trehalose concentration in the solution, the Δn value is much smaller than with other sugars. The disaccharide concentration of 0.5 mol% (~10 weight %) corresponds to typical concentrations of sugars used in many cryoprotective solutions. Trehalose is known to exhibit the strongest cryoprotective properties compared to other low molecular weight sugars, the explanation of which has long been a subject of debate among both biologists and physical chemists [49-55]. At the same time, a low difference refractive index of SMHs in trehalose solution means a small density contrast. And this makes SMHs less suitable for heterogeneous ice nucleation during solution cooling.
In addition, given the differences in the scattering capacity (Table 1 and Formula 6) and scattering intensity (Figure 3), the concentration of SMHs in a 0.5 mol% trehalose solution is by 2 orders of magnitude greater than, for example, in a similar sucrose solution. At a sufficiently deep cooling of the solution, when the driving force of crystallization makes possible the ice nucleation on SMHs, the more ice crystals are formed. With equal total mass of ice formed, the average crystal size in trehalose solution will be smaller compared to other solutions. This contributes to a less damaging effect on the biobject.
In modern approaches to cryopreservation, much effort is made to select mixtures of sugars (often together with penetrating cryoprotectants) to achieve the greatest effect on the processes of ice crystal formation and growth [56, 57]. However, this selection is mostly carried out empirically, with a focus on the result, without attempts to understand these processes at the fundamental physico-chemical level. The presence of SMHs in such solutions has never been taken into account, although they may act as crystallization centers or, conversely, as inhibitors of ice crystal growth. This, of course, requires further study using a larger number of substances and also in regimes of supercooling of solutions.
Conclusion
In aqueous solutions of four sugars - glucose, sucrose, maltose and trehalose - at concentrations from
0.5 to 1.5 mol%, stable submicron heterogeneities were revealed by light scattering methods. The intensity of light scattering in solutions becomes higher as far as the concentration of sugars increases. This points out to an increase in the numerical concentration of SMHs, whereas their sizes practically do not change. The differential refractive indices of SMHs relative to the average value in solutions have been determined: 0.001-0.01, which are much smaller than those typical of colloids. This explains the low observability of SMHs by the most experimental The values of the differential refractive indexes of SMHs can differ greatly between solutions of chemically and structurally similar organic molecules, such as disaccharides. At sugar concentrations of ~10 wt%, typical for cryoprotective solutions, the trehalose solution has a much lower SMH differential refractive index compared to the other sugars, which also means the lowest SMH density contrast in this solution. At the same time, the numerical concentration of SMH in trehalose solution is the highest. A possible role of SMHs in cryoprotection processes has been considered for the first time. An assumption has been made about the connection of the lowest differential refractive index of SMHs and their highest concentration in trehalose solution with the highest cryoprotective efficiency of trehalose compared to other low-molecular sugars.
Part of the work was performed using the equipment of the Optical Microscopy and Spectrophotometry Sector (https://www.pbcras.ru/services/tskp/ of the Pushchino Scientific Center for Biological Research of the Russian Academy of Sciences (PSCBR RAS).
Conflict of interest
The authors declare no conflict of interest.
References
- Vuks M. F., and Shurupova L. V. The scattering of light and phase transition in solutions of tertiary butyl alcohol in Opt Commun., 5 (4), 277-278 (1972). DOI: 10.1016/0030-4018(72)90096-X
- Beer C. W., and Jolly D. J. Comments on “the scattering of light and phase transition in solutions of tertiary butyl alcohol in water.” Opt Commun., 11 (2), 150-151 (1974). DOI: 10.1016/0030-4018(74)90205-3
- Iwasaki K., and Fujiyama T. Light-scattering study of clathrate hydrate formation in binary mixtures of tert-butyl alcohol and water. 2. Temperature effect. J Phys Chem., 83 (4), 463-468 (1979). DOI: 10.1021/ j100467a008
- Kostko A. F., Anisimov M. A., and Sengers J. V. Criticality in aqueous solutions of 3-methylpyridine and sodium bromide. Phys Rev E., 70 (2), 026118 (2004). DOI: 10.1103/PhysRevE.70.026118
- Jin F., Ye J., Hong L., Lam H., and Wu C. Slow relaxation mode in mixtures of water and organic molecules: supramolecular structures or nanobubbles? J Phys Chem B., 111 (9), 2255-2261 (2007). DOI: 10.1021/ jp068665w
- Kononov L. O. Chemical reactivity and solution structure: on the way to a paradigm shift? RSC Adv., 5 (58), 46718-46734 (2015). DOI: 10.1039/C4RA17257D
- Medzhitov R. A., Buchelnikov A. S., Lantushenko A. O., and Evstigneev M. P. Rationalizing DLS size distributions of fullerene conjugates. Fullerenes, Nanotub Carbon Nanostructures, 1-5 (2024). DOI: 10.1080/1536383X.2024.2392030
- Sedlák M. Large-scale supramolecular structure in solutions of low molar mass compounds and mixtures of liquids: I. Light scattering characterization. J Phys Chem B., 110 (9), 4329-4338 (2006). DOI: 10.1021/jp0569335
- Sedlák M. Large-scale supramolecular structure in solutions of low molar mass compounds and mixtures of liquids: II. Kinetics of the formation and long-time stability. J Phys Chem B., 110 (9, 4339-4345 (2006. DOI: 10.1021/jp056934x
- Sedlák M. Large-scale supramolecular structure in solutions of low molar mass compounds and mixtures of liquids. III. Correlation with molecular properties and interactions. J Phys Chem B., 110 (28, 13976-13984 (2006). DOI: 10.1021/jp061919t
- Subramanian D., Boughter C. T., Klauda J. B., Hammouda B., and Anisimov M. A. Mesoscale inhomogeneities in aqueous solutions of small amphiphilic molecules. Faraday Discuss., 167, 217-238 (2013). DOI: 10.1039/c3fd00070b
- Subramanian D., Klauda J. B., Collings P. J., and Anisimov M. A. Mesoscale phenomena in ternary solutions of tertiary butyl alcohol, water, and propylene oxide. J Phys Chem B., 118 (22, 5994-6006 (2014. DOI: 10.1021/jp4125183
- Subramanian D., Ivanov D. A., Yudin I. K., Anisimov M. A., and Sengers J. V. Mesoscale inhomogeneities in aqueous solutions of 3-methylpyridine and tertiary butyl alcohol. J Chem Eng Data., 56 (4), 1238-1248 (2011). DOI: 10.1021/je101125e
- Li Z., Cheng H., Li J., Jinkun H., Li Z., Boualem H., and Charles C. H. Large-scale structures in tetrahydrofuran–water mixture with a trace amount of antioxidant butylhydroxytoluene (BHT). J Phys Chem B., 115 (24, 7887-7895 (2011. DOI: 10.1021/jp203777g
- Bunkin N. F., Shkirin A. V., Lyakhov G. A., Kobelev A. V., Penkov N. V., Ugraitskaya S. V., and Fesenko E. E. Droplet-like heterogeneity of aqueous tetrahydrofuran solutions at the submicrometer scale. J Chem Phys., 145 (18, 184501 (2016. DOI: 10.1063/1.4966187
- Chaikov L. L., Kovalenko K. V., Krivokhizha S. V., Kudryavtseva A. D., Tareeva M. V., Tcherniega N. V., and Shevchenko M. A. Structure of water microemulsion particles: study by optical methods. Phys Wave Phenom., 27 (2), 87-90 (2019). DOI: 10.3103/S1541308X1902002X
- Orlova A. V., Andrade R. R., da Silva C. O., Zinin A. I., and Kononov L. O. Polarimetry as a tool for the study of solutions of chiral solutes. ChemPhysChem., 15 (1), 195-207 (2014). DOI: 10.1002/cphc.201300894
- Jawor-Baczynska A., Moore B. D., Lee H. S., McCormick A. V., and Sefcik J. Population and size distribution of solute-rich mesospecies within mesostructured aqueous amino acid solutions. Faraday Discuss., 167, 425-440 (2013). DOI: 10.1039/c3fd00066d
- Penkov N. V., Zhmurin V. A., Kobelev A. V., Fesenko (Jr.) E. E., and Penkova N. A. Dispersed, optical and concentration characteristics of submicron heterogeneities in aqueous solutions of sugars. J Mol Liq., 398, 124281 (2024). DOI: 10.1016/j.molliq.2024.124281
- Penkov N. V., Zhmurin V. A., Manokhin A. A., Kobelev A. V., and Penkova N. A. Capillary effects of submicron heterogeneities in aqueous solutions of sugars. The additional mechanism of microfluidics. J Mol Liq., 410, 125638 (2024). DOI: 10.1016/j.molliq.2024.125638
- Penkov N. V., Penkova N. A., Zhmurin V. A., and Pogorelov A. G. Natural submicron heterogeneities in aqueous solutions of ATP. Phys Wave Phenom., 32 (3), 178-186 (2024). DOI: 10.3103/S1541308X24700134
- Sedlák M., and Rak D. On the origin of mesoscale structures in aqueous solutions of tertiary butylalcohol: The mystery resolved. J Phys Chem B, 118 (10), 2726-2737 (2014). DOI: 10.1021/jp500953m
- Rak D., and Sedlák M. Solvophobicity-driven mesoscale structures: stabilizer-free nanodispersions. Langmuir, 39 (4), 1515-1528 (2023). DOI: 10.1021/acs.langmuir.2c02911
- Bunkin N. F., Lyakhov G. A., Shkirin A. V., Kobelev A. V., Penkov N. V., Ugraitskaya S. V., and Fesenko (Jr.) E. E. Study of the submicron heterogeneity of aqueous solutions of hydrogen-bond acceptor molecules by laser diagnostics methods. Phys Wave Phenom., 23 (4), 241-254 (2015). DOI: 10.3103/S1541308X15040019
- Bunkin N. F., Lyakhov G. A, Shkirin A. V., Krivokhizha S. V., Afonin A. A., Kobelev A. V., Penkov N. V., and Fesenko E. E. Laser diagnostics of the mesoscale heterogeneity of aqueous solutions of polar organic compounds. Phys Wave Phenom., 26 (1), 21-35 (2018). DOI: 10.3103/S1541308X18010041
- Bunkin N. F., Lyakhov G. A., Shkirin A. V., Ignatiev P. S., Kobelev A. V., Penkov N. V., and Fesenko E. E. Mesodroplet heterogeneity of low-concentration aqueous solutions of polar organic compounds. Phys Wave Phenom., 27 (2), 91-101 (2019). DOI: 10.3103/S1541308X19020031
- Cainelli G., Galletti P., and Giacomini D. Solvent effects on stereoselectivity: more than just anenvironment. Chem Soc Rev., 38 (4, 990-1001 (2009. DOI: 10.1039/b802815j
- Jin F., Li J., Ye X., and Wu C. Effects of pH and ionic strength on the stability of nanobubbles in aqueous solutions of α-cyclodextrin. J Phys Chem B, 111 (40),11745-11749 (2007). DOI: 10.1021/jp074260f
- Jin F., Ye X., and Wu C. Observation of kinetic and structural scalings during slow coalescence of nanobubbles in an aqueous solution. J Phys Chem B, 111 (46), 13143-13146 (2007). DOI: 10.1021/jp077190l
- Sedlák M., and Rak D. Large-scale inhomogeneities in solutions of low molar mass compounds and mixtures of liquids: Supramolecular structures or nanobubbles? J Phys Chem B, 117 (8), 2495-2504 (2013). DOI: 10.1021/jp4002093
- Häbich A., Ducker W., Dunstan D. E., and Zhang X. Do stable nanobubbles exist in mixtures of organic solvents and water? J Phys Chem B, 114 (20, 6962-69672010. DOI: 10.1021/jp911868j
- Subramanian D., and Anisimov M. A. Resolving the mystery of aqueous solutions of tertiary butylalcohol. J Phys Chem B, 115 (29, 9179-9183 (2011. DOI: 10.1021/jp2041795
- Rak D., Ovadová M., and Sedlák M. (Nonexistence of bulk nanobubbles: The role of ultrasonic cavitation and organic solutes in water. J Phys Chem Lett., 10 (15), 4215-4221 (2019). DOI: 10.1021/acs. jpclett.9b01402
- Bunkin N. F., and Bunkin F. V. Bubston structure of water and electrolyte aqueous solutions. Physics- Uspekhi., 59 (9, 846-865 (2016. DOI: 10.3367/UFNe.2016.05.037796
- Yurchenko S. O., Shkirin A. V., Ninham B. W., Sychev A. A., Babenko V. A., Penkov N. V., Kryuchkov N. P., and Bunkin N. F. Ion-specific and thermal effects in the stabilization of the gas nanobubble phase in bulk aqueous electrolyte solutions. Langmuir, 32 (43), 11245-11255 (2016). DOI: 10.1021/acs.langmuir.6b01644
- Bunkin N. F., Shkirin A. V., Penkov N. V., Goltayev M. V., Ignatiev P. S., Gudkov S. V., and Izmailov A. Yu. Effect of gas type and its pressure on nanobubble generation. Front Chem., 9, 630074 (2021). DOI: 10.3389/fchem.2021.630074
- Bunkin N. F., Shkirin A. V., Suyazov N. V., Babenko V. A., Sychev A. A., Penkov N. V., Belosludtsev K. N., and Gudkov S. V. Formation and dynamics of ion-stabilized gas nanobubble phase in the bulk of aqueous NaCl solutions. J Phys Chem B, 120 (7), 1291-1303 (2016). DOI: 10.1021/acs.jpcb.5b11103
- Georgalis Y., Kierzek A. M., and Saenger W. Cluster formation in aqueous electrolyte solutions observed by dynamic light scattering. J Phys Chem B, 104 (15), 3405-3406 (2000). DOI: 10.1021/jp000132e
- Penkov N. V. Application of terahertz time-domain spectroscopy to study the microheterogeneities of solutions: A case study of aqueous sugar solutions. Photonics, 10 (8), 887 (2023). DOI: 10.3390/photonics10080887
- Hagmeyer D., Ruesing J., Fenske T., Klein H.-W., Schmuck C., Schrader W., Piedade M. E. Minas da, and Epple M. Direct experimental observation of the aggregation of α-amino acids into 100–200 nm clusters in aqueous solution. RSC Adv., 2 (11), 4690-4696 (2012). DOI: 10.1039/c2ra01352e
- Rademacher T. W., Parekh R. B., and Dwek R. A. Glycobiology. Annu Rev Biochem., 57 (1), 785-838 (1988). DOI: 10.1146/annurev.bi.57.070188.004033
- Sanders L. M. Carbohydrate: Digestion, Absorption and Metabolism. In: Encyclopedia of Food and Health, Ed. by B. Caballero, P. M. Finglas, F. Toldra (Oxford, Academic Press, 2016), pp. 643-650. DOI: 10.1016/B978-0-12-384947-2.00114-8
- Wang C., Chantraine C., Viljoen A., Herr A. B., Fey P. D., Horswill A. R., Mathelié-Guinlet M., and Dufrêne Y. F. The staphylococcal biofilm protein Aap mediates cell–cell adhesion through mechanically distinct homophilic and lectin interactions. PNAS Nexus, 1 (5), 278 (2022). DOI: 10.1093/pnasnexus/pgac278
- Grzesik K., and Hoja-Łukowicz D. Rola glikanów w rozwoju i progresji nowotworu. Zastosowania kliniczne. Postepy Biochem., 67 (2), 104-116 (2021). DOI: 10.18388/pb.2021_385
- Jain N. K., and Roy I. Effect of trehalose on protein structure. Protein Sci., 18 (1), 24-36 (2008). DOI: 10.1002/pro.3
- Berne B. J., and Pecora R. Dynamic Light Scattering: With Applications to Chemistry, Biology, and Physics (Dover Publications, 1976).
- Landau L. D., and Lifshitz E. M. Fluid Mechanics. Course of Theoretical Physics. (2nd ed. Butterworth–Heinemann, 1987), Vol 6.
- Astle M. J., Beyer W. H., and Allen J. A. Van. Handbook of Chemistry and Physics, Weast R. C., ed. (CRC Press, 1984).
- Crowe L. M., Mouradian R., Crowe J. H., Jackson S. A., and Womersley C. Effects of carbohydrates on membrane stability at low water activities. Biochim Biophys Acta - Biomembr., 769 (1), 141-150 (1984). DOI: 10.1016/0005-2736(84)90017-8
- Ahmad E., and Aksoy M. Trehalose as a cryoprotective agent for the sperm cells: a mini review. Anim Heal Prod Hyg., 1 (2), 123-129 (2012). https://researchgate.net/publication/235719676_Trehalose_as_a_Cryoprotective_Agent_for_the_Sperm_Cells_A_mini_review
- Huang H., Zhao G., Zhang Y., Xu J., Toth T. L., and He X. Predehydration and ice seeding in the presence of trehalose enable cell cryopreservation. ACS Biomater Sci Eng., 3 (8), 1758-1768 (2017). DOI: 10.1021/acsbiomaterials.7b00201
- Crowe J. H., Crowe L. M., and Chapman D. Preservation of membranes in anhydrobiotic organisms: The role of trehalose. Science, 223 (4637), 701-703 (1984). DOI: 10.1126/science.223.4637.701
- Branca C., Magazù S., Maisano G., Migliardo F., Migliardo P., and Romeo G. α,α-Trehalose/Water solutions. 5. Hydration and viscosity in dilute and semidilute disaccharide solutions. J Phys Chem B, 105 (41), 10140-10145 (2001). DOI: 10.1021/jp010179f
- Kawai H., Sakurai M., Inoue Y., Chûjô R., and Kobayashi S. Hydration of oligosaccharides: anomalous hydration ability of trehalose. Cryobiology, 29 (5), 599-606 (1992). DOI: 10.1016/0011-2240(92)90064-9
- Heyden M., Bründermann E., Heugen U., Niehues G., Leitner D. M., Havenith M. Long-range influence of carbohydrates on the solvation dynamics of water—answers from terahertz absorption measurements and molecular modeling simulations. J Am Chem Soc., 130 (17), 5773-5779 (2008). DOI: 10.1021/ja0781083
- Yong K. W., Laouar L., Elliott J. A. W., Jomha N. M. Review of non-permeating cryoprotectants as supplements for vitrification of mammalian tissues. Cryobiology, 96, 1-11 (2020). DOI: 10.1016/j. cryobiol.2020.08.012
- Murray K. A., Gibson M. I. Chemical approaches to cryopreservation. Nat Rev Chem., 6 (8), 579-593 (2022). DOI: 10.1038/s41570-022-00407-4
License
Copyright (c) 2025 Никита Пеньков, В.А. Жмурин, Е.Е. Фесенко (мл.) (Автор)

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.